問題文
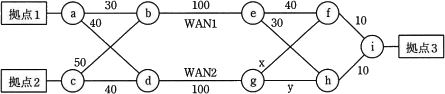
図は,OSPFを使用するルータa~iのネットワーク構成を示す。拠点1と拠点3の間の通信はWAN1を,拠点2と拠点3の間の通信はWAN2を通過するようにしたい。xとyに設定するコストとして適切な組合せはどれか。ここで,図中の数字は,OSPFコストを示す。
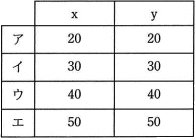
選択肢
問題の意図
OSPF(Open Shortest Path First)とは、リンクステート型(LSA)のルーティングプロトコルである。
簡単に言うと、他のノード(ルーター)と通信を行うことでルーティングテーブルを作成していく。
その際に、各経路のコストを計算する。OSPFでは、その経路が最小となるものが最適経路として選択される。
OSPFによる経路選択について理解があるかどうかを問う問題(だと思う。)
解法
まずはそれぞれの経路のコストを求めていく
拠点1→拠点3
WAN1を通った場合の経路とコスト
a→b→e→h→i = 30 + 100 + 30 + 10 = 170 … (1)
WAN2を通った場合の経路とコスト
a→d→g→f→i または a→d→g→h→i
a→d→g→f→i = 40 + 100 + x + 10 = 150 + x … (2)
a→d→g→h→i = 40 + 100 + y + 10 = 150 + y … (3)
拠点2→拠点3
WAN1を通った場合の経路とコスト
c→b→e→f→i または c→b→e→h→i
c→b→e→f→i = 50 + 100 + 40 + 10 = 200 ←こいつは既に負けているので除外
c→b→e→h→i = 50 + 100 + 30 + 10 = 190 … (4)
WAN2を通った場合の経路とコスト
c→d→g→f→i または c→d→g→h→i
c→d→g→f→i = 40 + 100 + x + 10 = 150 + x …(5)
c→d→g→h→i = 40 + 100 + y + 10 = 150 + y …(6)
拠点1と拠点3の間の通信はWAN1を,拠点2と拠点3の間の通信はWAN2を通過するようにしたい。
問題文より
とあるので、拠点1→拠点3、拠点2→拠点3がそれぞれ、指定されたWANを通るように方程式を作成していく。
拠点1から拠点3へは、WAN1を通りたいので
(1) < (2) AND (1) < (3)
=> 20 < x AND 20 < y
拠点2から拠点3へは、WAN1を通りたいので
(5) < (4) AND (6) < (4)
=> x < 40 AND y < 40
∴ 20 < x < 40 AND 20 < y < 40
これを満たす、選択肢は(イ)です。
いい感じに解けたぜ!やった。
以上



コメント